기본 정렬 알고리즘[선택, 삽입, 버블, 합병, 퀵]

[선택 정렬]

현재 위치의 값과 비교 값의 크기를 비교하여 크냐 작냐에 따라 정렬 우선순위가 정해지며, 정렬을 수행하는 알고리즘.

크기가 크냐에 따라 최소 선택 정렬과 최대 선택 정렬로 구분할 수 있다. 최소 선택 정렬은 오름차순으로 정렬되며, 최대 선택 정렬은 내림차순으로 정렬이 된다.

 

시간 복잡도 : O(n^2)

공간 복잡도 : O(n)

 

수행 과정 : 오름차순으로 정렬

1. i번째 인덱스에 가장 작은 값을 저장하기 위해 i + 1번째 인덱스부터 n번째 인덱스까지 i번째 인덱스와 비교하여 가장 작은 값의 위치 j를 탐색한다.
2. 가장 작은 값이 위치한 j번째 인덱스와 i번째 인덱스의 값을 스왑해준다.
3. i를 1 증가시켜 다음 인덱스에 저장될 값을 구해준다.
4. i가 n-1일때 까지 반복.

void selection_sort(vector<int> _v)
{
    for (int i = 0; i < _v.size() - 1; i++)
    {
        int min_num_idx = i;
        for (int j = i + 1; j < _v.size(); j++)
        {
            if (_v[min_num_idx] > _v[j])
            {
            	min_num_idx = j;
            }
        }
        
        int temp = _v[min_num_idx];
        _v[min_num_idx] = _v[i];
        _v[i] = temp;
    }
}

 

[삽입 정렬]

배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여, 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 알고리즘이다. 보통 1번째 인덱스부터 시작을 한다.

 

시간 복잡도 : O(n^2)

공간 복잡도 : O(n)

 

수행 과정 : 오름차순

1. 1번째 인덱스를 i로 하여 이를 기준으로 정렬을 시작한다.
2. j = i - 1부터 0까지 i번째 인덱스의 값이 들어갈 위치를 탐색해준다.
3. i번째 인덱스의 값이 j번째 인덱스의 값보다 작으면 두 값의 위치를 서로 바꿔준다.
4. i번째 인덱스의 값이 j번째 인덱스의 값보다 클때까지 반복한다.

vector<int> insert_sort(vector<int> _v)
{
    for (int i = 1; i < _v.size(); i++)
    {
    	int current = _v[i];
    	for (int j = i - 1; j >= 0 && current < _v[j]; j--)
    	{
    	    _v[j + 1] = _v[j];
    	    _v[j] = current;
    	}
    }

    return _v;
}

 

[버블 정렬]

버블 정렬은 매번 연속된 두개의 인덱스를 비교하여, 정한 기준의 값을 뒤로 넘겨 정렬하는 방식. 오름차순으로 정렬시 큰 값이 뒤로 이동하며, 1바퀴 돌 때 가장 큰 값이 맨 뒤에 저장된다. 따라서, 버블 정렬은 배열의 가장 마지막 인덱스부터 정렬이 되는 알고리즘이다.

 

시간 복잡도 : O(n^2)

공간 복잡도 : O(n)

 

수행 과정 : 오름차순

1. 삽입 정렬은 두개의 서로 이웃한 인덱스를 비교한다. 그렇기 때문에 계산상의 편의를 위하여 i = 0으로 시작하여 n - 1번의 반복과 함께 1번째 인덱스부터 비교가 시작된다.
2. j = 1 일때, j - 1번째 인덱스와 값을 비교하며, 인덱스의 값이 큰것이 뒤로 가게 된다.

vector<int> buble_sort(vector<int> _v)
{
    for (int i = 0; i < _v.size(); i++)
    {
        for (int j = 1; j < _v.size() - i; j++)
        {
    	    if (_v[j] < _v[j - 1])
    	    {
                int temp = _v[j];
                _v[j] = _v[j - 1];
                _v[j - 1] = temp;
    	    }
    	}
    }

    return _v;
}

 

[합병 정렬]

합병 정렬은 분할 정복방식으로 설계된 알고리즘이다. 큰 문제를 반으로 쪼개 문제를 해결해 나가는 방식으로, 분할은 배열의 크기가 1보다 작거나 같을때 까지 반복한다.

 

합병은 두 개의 배열을 비교하여, 기준에 맞는 값을 다른 배열에 저장해 나간다.

오름차순의 경우 배열 A, 배열 B를 비교하여 A에 있는 값이 더 작다면 새 배열에 저장해주고, A 인덱스를 증가시킨 후 A,B의 반복을 진행한다. 이는 A나 B중 하나가 모든 배열갑들을 새 배열에 저장할 때 까지 반복하며, 전부 다 저장하지 못한 배열의 값들은 모두 새 배열의 값에 저장해준다.

 

시간 복잡도 : O(nLogn)

공간 복잡도 : O(2n)

 

분할 과정

1. 현재 배열을 반으로 쪼갠다. 배열의 시작 위치와, 종료 위치를 입력받아 둘을 더한 후 2를 나눠 그 위치를 기준으로 나눈다.
2. 이를 쪼갠 배열의 크기가 0이거나 1일때 까지 반복한다.

합병 과정

1. 두 배열 A, B의 크기를 비교한다. 각각의 배열의 현재 인덱스를 i, j로 가정한다.
2. i에는 A배열의 시작 인덱스를 저장하고, j에는 B 배열의 시작 주소를 저장한다.
3. A[i]와 B[j]를 비교한다. 오름차순의 경우 이중에 작은 값을 새 배열 C에 저장한다. A[i]가 더 컸다면 A[i]의 값을 배열 C에 저장해주고, i의 값을 하나 증가시켜준다.
4. 이를 i나 j 둘중 하나가 각자 배열의 끝에 도달할 때 까지 반복한다.
5. 끝까지 저장을 못한 배열의 값을, 순서대로 전부 다 C에 저장한다.
6. C의 배열을 원래의 배열에 저장해준다.

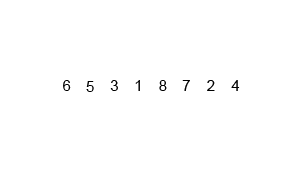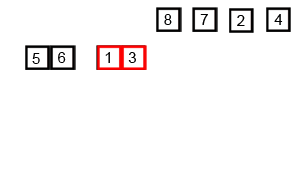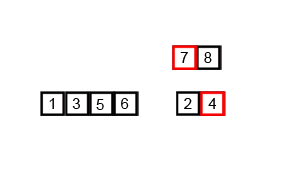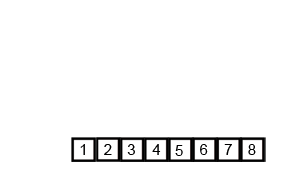
void merge(vector<int>& _v, int _s, int _e, int _m)
{
    vector<int> result;
    int i = _s, j = _m + 1;

    while (i <= _m && j <= _e)
    {
        if (_v[i] < _v[j])
        {
            result.push_back(_v[i]);
            i++;
        }
        else if (_v[i] > _v[j])
        {
            result.push_back(_v[j]);
            j++;
        }
    }

    while (i <= _m)
        result.push_back(_v[i++]);
    while (j <= _e)
        result.push_back(_v[j++]);

    int copy = 0;
    for (int k = _s; k <= _e; k++)
    {
        _v[k] = result[copy++];
    }
}

void merge_sort(vector<int>& _v, int _s, int _e)
{
    if (_s < _e)
    {
        int m = (_e + _s) / 2;

        // divide
        merge_sort(_v, _s, m);
        merge_sort(_v, m + 1, _e);

        // merge
        merge(_v, _s, _e, m);
    }
}

 

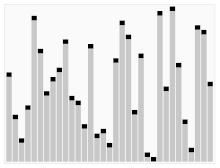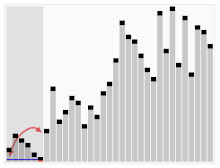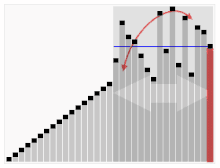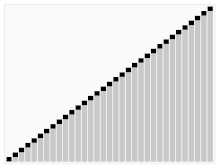
[퀵 정렬]

퀵정렬 또한 분할 정복을 이용하여 정렬을 수행하는 알고리즘이다. Pivot을 설정한 다음, 이 값을 기준으로 작은 값은 왼쪽, 큰 값은 오른쪽으로 옮기는 방식으로 정렬을 진행한다. 이를 반복하여 분할된 배열의 크기가 1이되면 배열이 모두 정렬된 것이다. 퀵 정렬은 이미 정렬된 리스트에 대하여 퀵 정렬을 실행하는 경우가 최악의 경우인데, 이때 분할이 N만큼 일어나므로 시간 복잡도는 O(n^2) 이다.

 

시간 복잡도 : O(nLogn)

 

수행 과정 : 오름차순

1. 리스트 안에 있는 한 요소를 선택한다. 이렇게 고른 원소를 Pivot 이라고 한다.
2. Pivot을 기준으로 이보다 작은 요소들은 모두 왼쪽으로 옮겨지고, 큰 요소들은 오른쪽으로 옮겨진다.
3. Pivot을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬한다.
   1. 분할된 부분 리스트에 대하여 순환 호출을 이용하여 정렬을 반복한다.
   2. 부분 리스트에서도 다시 Pivot을 정하고 이를 기준으로 2개의 부분 리스트로 나누는 과정을 반복한다.
4. 부분 리스트들이 더 이상 분할이 불가능할 때까지 반복한다.(리스트의 크기가 0이나 1이 될 때까지 반복한다.)

void quick_sort(vector<int>& _v, int _s, int _e)
{
    int pivot = _v[_s];
    int temp_s = _s, temp_e = _e;

    while (_s < _e)
    {
        while (pivot <= _v[_e] && _s < _e)
            _e--;
        if (_s > _e)
            break;

        while (pivot >= _v[_s] && _s < _e)
            _s++;
        if (_s > _e)
            break;

        int temp = _v[_s];
        _v[_s] = _v[_e];
        _v[_e] = temp;
    }

    int temp = _v[_s];
    _v[_s] = _v[temp_s];
    _v[temp_s] = temp;

    if (temp_s < _s)
        quick_sort(_v, temp_s, _s - 1);
    if (temp_e > _e)
        quick_sort(_v, _s + 1, temp_e);
}

 

[성능 순서]

O(1) < O(longn) < O(n) < O(nlongn) < O(n^2) < O(n^3) < O(2n)